지난 글에서 다루었던 코호트 분석에 이어서, 이번에는 고객 분류의 한 종류인 RFM 기법에 대해 알아보자! 😎
1. RFM 분석이란?
RFM 분석은 고객의 가치를 분석하기 위한 기법으로, 정확히 말하면 고객을 R-F-M의 차원에서 등급을 매기는 분석을 의미한다. RFM 분석은 Optimal Selection for Direct Mail(1995)이라는 이메일 캠페인에 관한 논문에서 최초로(?) 다뤄졌다고 알려져 있다. 다만 이미 논문에서도 RFM 기법을 최초 소개하는 것이 아닌, 이미 널리 쓰이고 있다고 언급하기 때문에 실제 쓰임은 더 오래되었을 것이다.
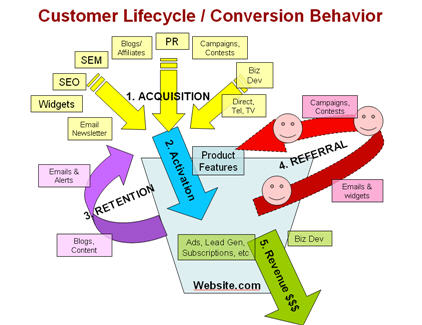
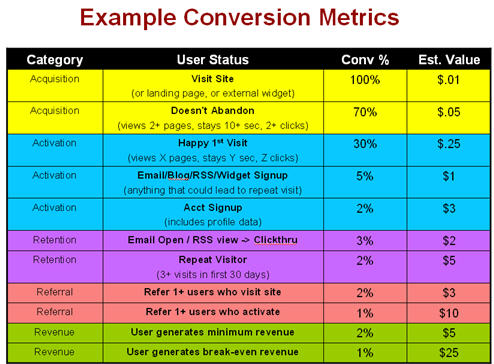
대표적인 RFM의 구현법에서, R-F-M은 각각 다음을 의미한다. R이 가장 중요하다고 여겨지며, 그 다음이 F와 M이다.
- Recency: 고객이 얼마나 최근에 구매를 했는가?
- Frequency: 고객이 (주어진 기간 동안) 얼마나 자주 구매를 했는가?
- Monetary: 고객이 (주어진 기간 동안) 구매에 얼마를 지출하였는가?
이미지 출처: https://clevertap.com/blog/rfm-analysis/
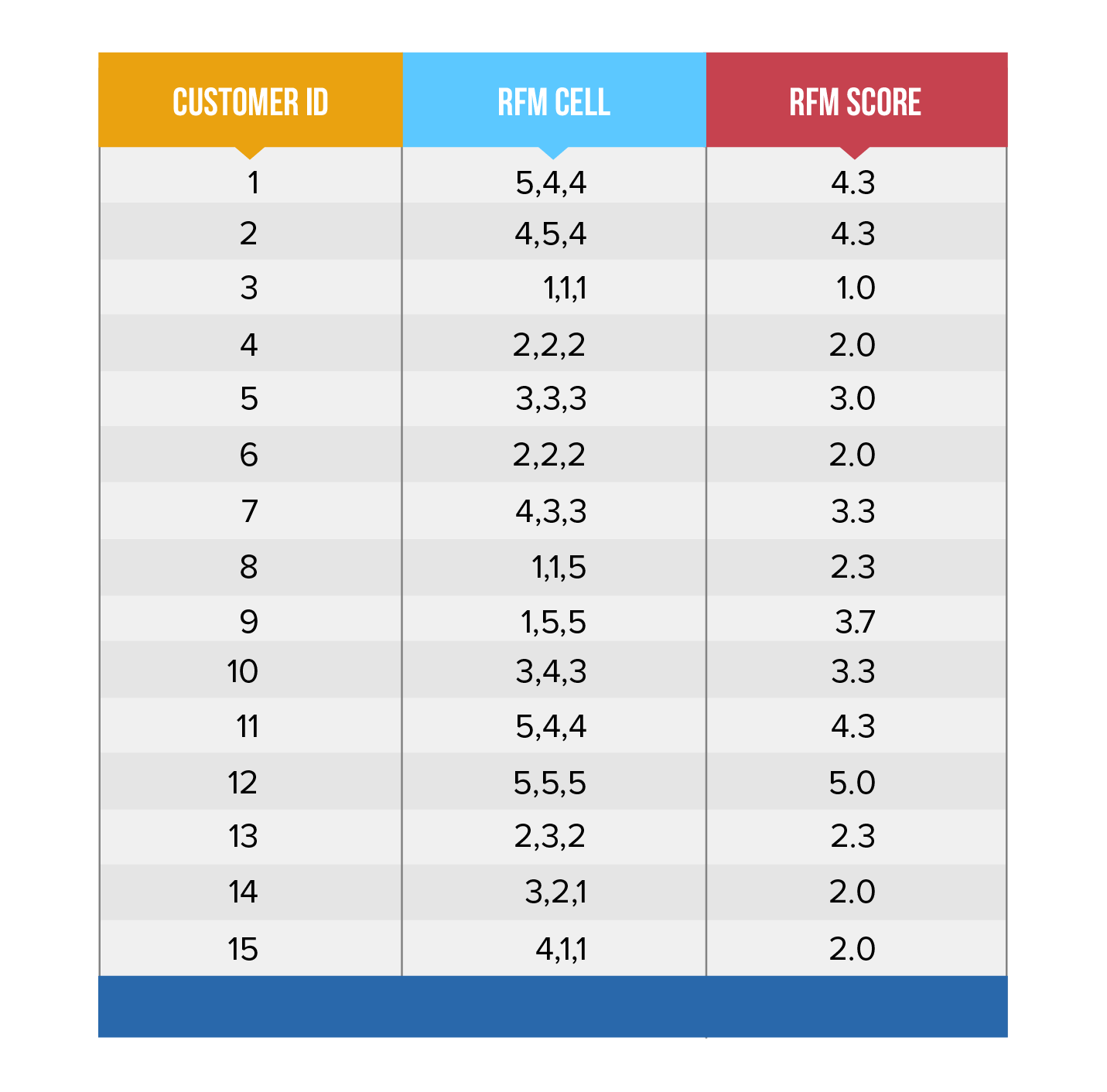
즉, RFM 분석(RFM Analysis / RFM Scoring)을 다시 풀어서 설명하자면 각각의 R-F-M 차원에서 개별 고객들이 얼마나 잘 하고 있는지 등급을 매기는 기법을 의미한다. 이 설명이 RFM의 전부일 만큼 RFM은 계산이 간단하고 직관적이다. 이제 RFM 기법을 적용하는 과정을 알아보자.
RFM은 오래된 기법이고 직관적인 방법인 만큼 구현 방식이 다양하게 소개되어있다. 여기서는 가장 일반적으로 받아들여지는 RFM 구현을 소개하고, 아래에서 여러가지 방식들도 소개하겠다.
2. RFM 분석 프로세스
일반적인 RFM 분석은 아래의 프로세스로 진행된다.
- RFM 분석의 기본이 되는 데이터를 준비한다. (고객ID, 최근 구매 날짜, 특정기간 내 구매 횟수, 특정기간 내 구매 금액)
- R-F-M 개별 등급의 카테고리 수를 정한다. 일반적으로 5개 등급을 부여하는데, 이렇게 되면 각각 5개 등급씩 총 5x5x5=125개의 등급 조합이 생긴다. (이 개별 조합을 셀cell이라고 부른다.)
- 이제 개별 고객을 각 등급에 할당해야 한다. 가장 단순하게는, R-F-M 개별에서 점수가 높은 순으로 정렬한 뒤, 5분위로 나누어 가장 높은 등급이 5가 되도록 한다.
- Recency는 최근 구매 날짜가 가까운 순서로
- Frequency는 구매 횟수가 가장 큰 순서로
- Monetary는 구매 총액이 가장 큰 순서로 (또는 구매 평균 금액)
- R-F-M에 대해 모두 등급을 할당하면, 이렇게 개별 고객에게 만들어진 조합이 RFM 셀이 된다. ex) 5-1-3, 5-1-4, 1-3-5
여기까지는 RFM 세그멘테이션을 진행하는 방법이고, 더 나아가 마케팅적 적용은 아래의 단계를 거칠 수 있다. 해당 내용은 이 글을 옮긴 내용이다. (원문과 세그멘테이션 구현 방식은 다르므로 주의, 글의 원래 내용은 Arthur Hughes의 Strategic database marketing에서 나온다)
- 만약 이메일 마케팅을 진행한다면, 전체 고객 중 테스트 표본을 선발한다. 이 테스트 표본에 대해 RFM 세그멘테이션을 해둔다.
- 테스트 표본에 대해 이메일 마케팅을 진행하고 결과(전환과 비용)를 기록한다.
- 손익분기점이 되는 응답률, 또는 타겟 비율을 선정한다.
- 만약 손익분기점이 되는 응답률이 목표라면 응답률은 (응답당 비용/응답당 수익)으로 계산할 수 있다.
- 테스트 표본의 RFM 셀별 응답률을 계산하고, 위에서 선정한 응답률보다 높은 셀만 타겟으로 선정한다.
- 만약 표본이 전체 고객 집단을 잘 대표한다면 표본의 셀과 전체 고객의 셀은 유사한 결과를 보일 것이다. 따라서 전체 고객에서 RFM 세그멘테이션을 다시 진행하고, 타겟 셀에만 선별적인 이메일 마케팅을 진행한다.
3. RFM 분석의 의미, 한계점
RFM 분석의 기본 아이디어는 파레토 법칙에 있다. 상위 20%의 고객에게서 80%의 수익이 나온다는 부분에 집중하기 때문에 기본적으로는 우수 고객들에게 집중하는 분석이다. 거기에 더하여, 과거 구매 데이터를 기반으로 하기 때문에 구매하지 않는 대다수의 고객들은 마케팅의 대상에서 제외된다.
그럼에도 과거에 널리 쓰였던 이유는 RFM 분석의 쉬운 적용과 직관성에 있다. 구매 데이터만 있다면 누구든 손쉽게 RFM 세그멘테이션을 진행할 수 있고, RFM 각 디멘션이 나타내는 바가 직관적이기 때문이다. 다만 여전히 과거 데이터를 기반으로 분류하는 것에서 그치기 때문에 예측 분석 기법이 발달된 지금은 선호도가 떨어진다고 생각된다.
RFM의 장점은 위에서 언급한 것처럼 명확하기 때문에 몇가지 한계점을 나열하자면 아래와 같다. 출처는 A review of the application of RFM model, 2010.
- R-F-M 변수간 상호 독립성이 보장되지 않기 때문에 중복(redundancy, double counting) 이슈가 있다. 즉, Frequency가 높은 고객은 자연스레 Monetary도 높기 때문에 변수간 독립성이 성립되기 어렵다.
- 고객 풀을 나누는 데는 좋은 기법이지만, 마케팅 캠페인에 적용하기에는 훨씬 더 나은 예측 기법이 많다. 왜냐하면 RFM은 결국 구매에 관해 점수를 매기는 것이지 특정 마케팅 전환(ex, 메일의 응답률)에 대한 점수를 매긴 것이 아니기 때문이다.
- 위와 비슷한데, RFM은 현재 온라인 커머스 시장에 있는 무수한 고객 행동 데이터를 활용하지 못한다. 오직 구매 데이터만을 활용할 뿐이다.
- RFM을 통해서는 앞으로 새로 등장할 고객들에 대한 예측을 할 수 없다.
- 산업마다 각 R-F-M이 갖는 중요도가 다르지만 이들이 정량적으로 측정되기 어렵다.
4. RFM 구현의 다양성
RFM 분석은 구현이 쉬운 만큼 구현 방법도 매우 다양하다. 위에서 언급한 A review… 논문에서 이러한 다양한 구현법에 대해 언급해주는데 몇 가지를 알아보고 파이썬을 통해 직접 RFM 세그멘테이션을 구현해보도록 하겠다.
1) 개별 등급을 나누는 방법
개별 등급을 나누는 방법은 크게 두 가지가 있다. Thoughts on RFM scoring, John Miglautsch, 2000을 참고했다.
Customer Quintile Method
위 프로세스에서 소개한 방법으로, 단순히 크기로 정렬하여 20%씩 할당하는 방식이다. 상위 20%는 5등급을, 하위 20%는 1등급을 받게 된다. (RFM에서는 일반적으로 등급이 클수록 좋다)
이 방식은 간편하지만 한계점들이 있다.
- 일반적으로 구매 빈도(F)는 1회인 고객이 많게는 60%까지도 될 수 있다. 이러한 경우 동일한 행동을 한 고객들이 서로 다른 등급으로 취급될 수 있다. (spill over, bracket creep problem)
- Relative Sensitivity: 5등급의 고객만 살펴볼 때, 이들은 상위 20%~0%까지라고 표현할 수 있다. 이때, 상위 0%와 20%는 행동값이 크게 다를 수 있는데, 이들이 같은 등급에 묶이는 문제가 발생한다. 마찬가지로, 상위 20%와 4등급의 상위 21% 고객의 행동값은 비슷하지만, 이들을 임의로 쪼개는 경향도 발생한다. 이를 논문에서는 상대적 민감성이라고 표현한다.
Behavior Quintile Method (by John Wirth)
고객의 행동값을 기준으로 5분위수를 만드는 방법이다. 논문에서는 위에서 소개한 고객 5분위수 방법처럼 정렬을 하되 등급간 Monetary의 합이 같도록 비율을 조정한다고 나와있는데, R-F-M 각각의 설명에서는 분류한 방식이 약간씩 다르다. 글에서는 각각의 설명을 따르도록 하겠다.
Recency
일반적으로는 달력 기반 방식을 쓰는 게 선호된다. Wirth는 0-3개월/4-6개월/7-12개월/13-24개월/25개월이상의 Recency 등급을 제안했다.
Frequency
그럼에도 여전히 구매 빈도(F)가 문제가 된다. 여기서 Ted Miglautsch가 새로운 기법을 제안하는데, 이 프로세스는 아래와 같다.
- 1회 구매자들에게는 1등급을 준다.
- 1등급을 제외하고, 남은 고객들의 빈도를 평균내어 평균보다 낮은 그룹에게 2등급을 준다.
- 반복하여 4등급까지 만들고, 남은 고객들은 5등급을 할당한다.
Monetary
5등급에 속한 5명의 고객이 총 100만원의 매출을 만들었다면 1등급은 100명의 고객이 100만원의 매출을 만드는 식으로 할당한다.
2) R-F-M 등급의 의존성
일단 의존성이라고 표현했는데, 두가지 방식을 설명하면 다음과 같다.
- a. R/F/M 개별로 등급을 매긴 뒤, 단순히 등급을 묶는 방식.
- b. R 등급을 매긴 뒤, R 등급의 1~5등급별로 F 등급을 매긴다. 마찬가지로 RF 등급쌍별로 M 등급을 매긴다.
즉 a 방법은 각 차원을 독립적으로 구성하고, b 방법은 앞의 차원에 의존적이게 구성이 된다. a의 장점은 간단하고 모든 셀이 동일한 사이즈로 구성된다는 점이고, b의 장점은 차원을 연계하여 상대적인 위치를 알 수 있다는 점인 것 같다.
예를 들어, 5-1-3 고객과 1-1-3 고객이 있다고 가정해보자. a 방식에서는 두 고객 모두 빈도(F) 점수가 1점이며, 실제로도 같은 수준의 빈도를 가지고 있을 것이다. b 방식에서는 그렇지 않다. 5-1-3 고객은 가장 최근에 방문한(R=5) 고객들 중 상대적으로 빈도가 낮은 고객 그룹이며, 1-1-3 고객은 아주 예전에 방문한(R=1) 고객들 중 상대적으로 빈도가 낮은 고객 그룹이 된다.
3) RFM 점수 만들기
RFM 세그멘테이션을 진행했다면 최종적으로 RFM 점수를 만들어 고객별 순위를 매길 수 있다. 이 단계는 선택적으로 진행하면 되고 아래의 구현 방식들이 있다.
- a. 단순히 R/F/M의 점수를 더한다. 5-5-5이면 15점이 된다.
- b. Judgment based RFM (also known as Hard-Coding) 개별로 가중치를 준다. 이 방식은 도메인별로 마케터의 재량에 따라 가중치를 줄 수 있도록 해준다.
5. RFM 분석 해보기
실제 데이터로 RFM 분석을 해 볼 시간이다. 데이터는 지난번 코호트 분석에 관한 글에서 썼던 것을 사용한다. 단, RFM 분석은 셀마다 어느정도 표본이 필요하기 때문에 1000명이 아닌 10000명씩 샘플링한다! 해당 데이터는 여기서 바로 받을 수도 있다.
앞서 소개한 여러가지 방법들 중, 아래의 방법을 사용한다.
- 데이터가 5개월동안의 이벤트를 포함하기 때문에 Recency 값은 (1주/2주/3주/4주/4주+)로 등급을 나눈다. 이커머스에서 주로 사용하는 전환 기준인 28일을 기준점으로 삼았다. 날짜 계산의 기준은 데이터의 마지막 날짜인 2월 29일로 한다.
- Frequency는 4번에서 소개한 Ted Miglautsch의 방법을 사용한다. 기준 기간은 데이터 전체(5개월)로 하겠다.
- Monetary는 단순히 크기순으로 5분위수를 나누도록 하겠다. (customer quintile method) 기준 기간은 위와 마찬가지.
1) 구매 데이터 불러오기
일단 sqlite에 새롭게 1만 샘플 데이터를 넣자. 파일별 고유 유저 1만 명을 샘플링한 것이기 때문에 실제 사이즈는 80만 개의 행이 조금 넘는다.
import sqlite3
# 일반적으로 connect는 host에 연결하는 행위이지만, SQLite은 곧바로 DB에 연결한다.
con = sqlite3.connect('ecommerce10000.db')
# 명령어를 실행해주기 위한 커서 선언
cur = con.cursor()
# event 테이블을 만들어준다. 일단 모두 text 타입으로 선언한다.
cur.execute("""
CREATE TABLE events
(event_time text, event_type text, product_id text, category_id text, category_code text, brand text, price text, user_id text, user_session text)
""")
import pandas as pd
# 아까 만든 데이터를 불러온다.
data = pd.read_csv('ecommerce_cosmetics_sampled_10000.csv')
lists = []
# 튜플 형태로 리스트에 넣어준다
for idx, row in data.iterrows():
lists.append(tuple([*row.values]))
# executemany를 통해 한 번에 데이터를 넣는다
cur.executemany("""INSERT INTO events VALUES (?, ?, ?, ?, ?, ?, ?, ?, ?)""",lists)
# 트랜잭션을 수행하는 모든 함수는 반드시 커밋을 해줘야 실제 트랜잭션이 수행된다
con.commit()
# 데이터 쿼리
cur.execute("""
SELECT
user_id,
DATE(SUBSTR(event_time, 1, 10)) AS event_time, -- 날짜로 변경해준다
price
FROM events
WHERE event_type = 'purchase'
LIMIT 1
""").fetchall()
[('380113376', '2019-12-01', '0.95')]
(사용자id, 날짜, 구매금액) 순으로 하나의 레코드만 살펴보았다. 여기에 추가적으로 필요한 데이터는 이 상태로 데이터를 불러와서 파이썬으로 작업을 해도 되는데, 나는 쿼리를 통해 필요한 데이터를 최대한 만들어두도록 하겠다.
문제는 현재 데이터가 주문당 데이터가 아닌, 개별 품목별 데이터라는 점이다. 따라서 1회 주문에서 A, B, C 세 상품을 구매했어도 세 개의 레코드로 분리되어 저장되어있다. 실제 raw data가 어떤 의미로 개별 저장되었는지는 알 수 없지만, 최대한 ‘주문당’ 데이터가 되도록 사용자별로 같은 (event_time, user_session) 쌍은 하나의 주문으로 취급하도록 하겠다.
cur = con.cursor()
# 데이터 쿼리
results = cur.execute("""
WITH
base AS (
SELECT
user_id,
user_session,
event_time,
price
FROM events
WHERE event_type = 'purchase'
)
,per_order AS (
SELECT
user_id,
user_session,
event_time,
SUM(price) AS order_price,
COUNT(*) AS order_item_cnt
FROM base
GROUP BY user_id, user_session, event_time
)
,rfm AS (
SELECT
user_id,
CAST(JulianDay('2020-02-29') - JulianDay(MAX(DATE(SUBSTR(event_time, 1, 10)))) AS INTEGER) AS recency, --SQLite은 datediff 함수가 없다
COUNT(*) AS frequency,
SUM(order_price) AS monetary
FROM per_order
GROUP BY user_id
)
SELECT * FROM rfm
""").fetchall()
con.close()
results[:1]
[('101779631', 32, 1, 41.45)]
이제 뽑아낸 데이터를 pandas를 활용해 데이터프레임으로 바꾸고, 각 데이터의 분포를 확인해보자.
import pandas as pd
df = pd.DataFrame(results, columns=[i[0] for i in cur.description])
df.hist()
array([[<AxesSubplot:title={'center':'recency'}>,
<AxesSubplot:title={'center':'frequency'}>],
[<AxesSubplot:title={'center':'monetary'}>, <AxesSubplot:>]],
dtype=object)
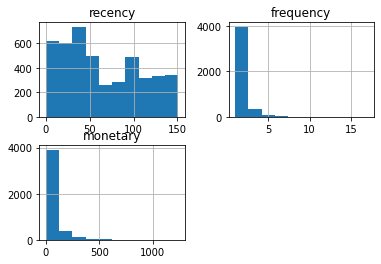
Recency는 비교적 골고루 분포하고 있고, Frequency는 예상대로 왼쪽으로 매우 치우쳐져 있는 것을 확인할 수 있다.
2) R-F-M 등급 부여하기
이제 개별 사용자에 대해 RFM 등급을 부여한다. 위에서 언급한대로 각각 적용하는 방식이 다르므로, 개별 함수를 만들어서 적용해줄 예정이다.
def recency(r):
if r <= 7:
return 5
elif r <= 14:
return 4
elif r <= 21:
return 3
elif r <= 28:
return 2
else:
return 1
# 개별 값에 대해 반복하기 때문에 map 함수
df['R'] = df['recency'].map(lambda x: recency(x))
df[['recency', 'R']].head(3)
|
recency |
R |
| 0 |
32 |
1 |
| 1 |
29 |
1 |
| 2 |
48 |
1 |
def frequency(f):
# 원본을 건드리지 않기 위해 새로 만듦
s = pd.Series([0 for _ in range(len(f))])
# 빈도가 1이면 1등급을 준다
s[f == 1] = 1
state = 2
while state <= 4:
# 아직 등급이 부여되지 않은 값들에 대해(값이 0), 평균보다 작은 값에 등급을 부여한다
s[(s == 0) & (f < f[s == 0].mean())] = state
state += 1
# 남은 것들은 5등급을 준다
s[s==0] = 5
return s
# 전체 값에 대해 접근하기 때문에 Series 전체를 함수에 넘김
df['F'] = frequency(df['frequency'])
df[['frequency', 'F']].head(3)
|
frequency |
F |
| 0 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
3 |
3 |
def monetary(m):
# copy를 만들어서 오름차순 정렬한다
s = m.copy()
qc = pd.qcut(s, 5, labels=False)
return (qc + 1)
df['M'] = monetary(df['monetary'])
df[['monetary', 'M']].head(3)
|
monetary |
M |
| 0 |
41.45 |
3 |
| 1 |
36.34 |
3 |
| 2 |
125.97 |
5 |
3) RFM 분포 살펴보기
이제 등급 부여가 모두 완료되었다. 완성된 모습을 살펴보자.
df['Cell'] = df['R'].map(str) + df['F'].map(str) + df['M'].map(str)
df.head()
|
user_id |
recency |
frequency |
monetary |
R |
F |
M |
Cell |
| 0 |
101779631 |
32 |
1 |
41.45 |
1 |
1 |
3 |
113 |
| 1 |
103274988 |
29 |
1 |
36.34 |
1 |
1 |
3 |
113 |
| 2 |
104808268 |
48 |
3 |
125.97 |
1 |
3 |
5 |
135 |
| 3 |
107945915 |
0 |
4 |
479.00 |
5 |
3 |
5 |
535 |
| 4 |
111782974 |
125 |
1 |
6.95 |
1 |
1 |
1 |
111 |
df.groupby(['R']).agg({'user_id': 'count'})
|
user_id |
| R |
|
| 1 |
3328 |
| 2 |
259 |
| 3 |
283 |
| 4 |
254 |
| 5 |
334 |
df.groupby(['F']).agg({'user_id': 'count'})
|
user_id |
| F |
|
| 1 |
3242 |
| 2 |
715 |
| 3 |
359 |
| 4 |
96 |
| 5 |
46 |
예상대로 1등급(1회 구매자) 인원이 60%를 넘는다.
df.groupby(['M']).agg({'user_id': 'count', 'monetary': 'sum'})
|
user_id |
monetary |
| M |
|
|
| 1 |
892 |
9226.76 |
| 2 |
891 |
19309.39 |
| 3 |
892 |
34033.14 |
| 4 |
891 |
55043.85 |
| 5 |
892 |
166014.13 |
4) RFM 시각화
만들어둔 RFM 분류를 잘 활용하기 위해 시각화를 진행해보자. Visualizing RFM Segmentation을 참고하였다.
우선 R-F 행렬을 만들어보자. RFM을 동시에 시각화하면 3차원으로 표현해야 하는데, 그렇게 되면 가독성이 상당히 떨어지기 때문에 대개 2차원으로 살펴본다.
rf_matrix = df.groupby(['R', 'F']).agg({
'user_id': 'count',
'monetary': 'sum'}).reset_index()
rf_matrix['avg_sales'] = rf_matrix['monetary']/rf_matrix['user_id']
이 행렬을 아래처럼 피벗해준다. sort_index를 거꾸로 하여 우측 상단으로 갈수록 좋은 등급을 나타낼 수 있도록 해준다. 피벗 이후에는 색상까지 입힌다. matplotlib으로 시각화를 해도 되지만, 이렇게 행렬 기반 시각화는 판다스 데이터프레임 내에서 하는 게 편해서 그냥 진행했다.
rf_pivot = rf_matrix\
.pivot(index='F', columns='R', values='user_id')\
.fillna(0)\
.sort_index(ascending=False)
rf_pivot\
.style\
.background_gradient(cmap ='Blues', axis=None, low=0.2)
| R | 1 | 2 | 3 | 4 | 5 |
| F | | | | | |
| 5 |
13 |
2 |
5 |
13 |
13 |
| 4 |
32 |
8 |
16 |
20 |
20 |
| 3 |
192 |
28 |
41 |
43 |
55 |
| 2 |
472 |
57 |
63 |
46 |
77 |
| 1 |
2619 |
164 |
158 |
132 |
169 |
이 테이블은 R-F 등급별 속한 사용자 수를 나타낸다. 예상대로 1-1이 상당히 많고, 높은 등급으로 갈수록 사용자가 희박해진다. 데이터 수가 적을수록 RFM의 분류를 진행하는 과정도 상당히 껄끄러워지고, 얻어갈 수 있는 인사이트도 줄어든다. 이번 예시에서는 어느정도 규모가 있는 데이터 셋을 사용하였기 때문에 이러한 어려움이 생기지는 않았다.
그 다음으로는 R-F 등급별 평균 구매 금액을 살펴본다. 전체 구매 금액으로 보면 당연히 사용자가 많은 1-1 그룹이 압도적이기 때문에, 평균 구매 금액을 보는 것이다.
rf_pivot = rf_matrix\
.pivot(index='F', columns='R', values='avg_sales')\
.fillna(0)\
.sort_index(ascending=False)
rf_pivot\
.style\
.background_gradient(cmap ='Blues', axis=None, low=0.2)
| R | 1 | 2 | 3 | 4 | 5 |
| F | | | | | |
| 5 |
363.550769 |
262.710000 |
514.260000 |
418.566154 |
316.460769 |
| 4 |
189.534063 |
403.881250 |
256.005625 |
319.256000 |
298.229000 |
| 3 |
142.825156 |
133.373929 |
158.582195 |
162.031163 |
153.661091 |
| 2 |
86.742373 |
84.342281 |
103.742222 |
76.111522 |
92.381688 |
| 1 |
38.107690 |
41.905305 |
41.418481 |
36.477879 |
38.424497 |
예상대로 등급이 높아질수록(5-5) 평균적으로 지출하는 금액이 크다. 여기서 몇가지 셀에 대한 추론을 해보자면 아래와 같을 수 있겠다.
- (R=1, F=5): 한동안 자주 구매하다가 방문한 지 매우 오래된 고객. 재방문 쿠폰을 제시해보자
- (R=3, F=5): 한동안 자주 구매하다가 방문한 지 오래된 고객. 평균 지출 금액이 가장 크다. 잠재적인 최고 고객이므로 적극적으로 마케팅을 해서 R 등급을 끌어올리자
- (R=5, F=5): 최근까지도 들어왔고 구매도 자주하는 고객. 충성고객으로 놓쳐서는 안 된다. 꾸준한 관리가 필요
이러한 컨셉은 clevertap이라는 마케팅 솔루션 블로그에서 참고했다. 더 나아가, 커머스마다 해당 패턴은 매우 다양할 것이므로 다양한 해석이 가능해진다.
5) RFM을 가지고 무엇을 해야할까
또 어떤 분석을 할 수 있을까? 결국 세그멘테이션의 한 종류인 RFM의 핵심도 그룹(cell)간의 차이점을 발견하고 그 차이에 맞는 마케팅을 적용하는 것일 것이다.
- 위에서는 그룹별 방문자수, 평균지출금액만 살펴보았지만 그 외의 요소들을 볼 수도 있다. 앞선 예시처럼 고객별 캠페인 응답률을 시각화하여 그룹별 차이를 볼 수도 있다.
- 전체적인 윤곽을 보고, 지나치게 몰려있는 셀이 있다면 해당 셀을 drill down하여 원인을 파악해볼 수 있다.
- 시간에 따른 RFM 분포의 변화를 살펴보고, 캠페인의 방향이 의도대로 가는지 확인할 수 있다.
6. 마치며
RFM 분석에 관해 정리하며 쓰다보니 글이 길어진 것 같다. 그래도 내가 예전에 구현하며 어려움을 겪었던 부분들이 많았기에 해당 부분을 더 집중적으로 다룰 수 있었다. 특히 처음 구현하는 입장에서는 찾아보는 RFM마다 적용하는 방식이 다르기에 뭐가 맞지라는 의문이 많이 드는데, 그러한 부분들을 짚고 넘어갈 수 있어서 만족한다 😎 . 다음에는 세그멘테이션에 관한 좀 더 브로드한 내용을 다루거나 마케팅 성과 측정에 관한 이야기를 해볼까 한다 😙